Quantum numbers and Differential Equations

I wanted to write up an introductory description of the Standard Model of particle physics, but the project has gotten out of hand as I want to start from first principles and I forget that from there, the trail is long.

Feynman Diagrams for the Masses (part 2)

In part 1, we briefly discussed how Feynman diagrams show up in QFT with an example taken from QED (quantum electrodynamics). The calculation for the first order correction to the photon propagator (i.e. vacuum polarization) turned out to be a rather messy integral:

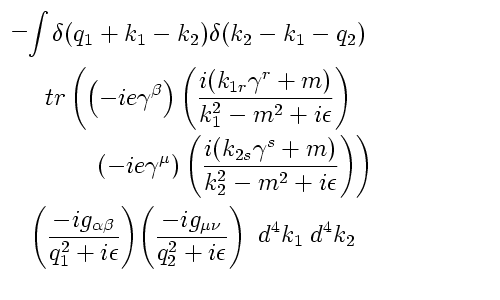
QFT’s little Infinity Problem

This is a mess because it (a) involves the trace of a product of four 4×4 matrices, (b) requires eight definite integrals, each from , and (c) gives infinity. Of these problems, the worst was the fact that the calculation gives infinity. This would make one conclude that the theory was nonsense, but there were some other calculations that worked, and what’s more important, the results of certain calculations could be evaluated as and k was a number which gave an excellent match to experiment.

Feynman Diagrams for the Masses (part 1)

If you want to win a Nobel Prize in Physics by finding the unified field theory, it’s pretty obvious that you will have to learn how to make Quantum field theory (QFT) calculations. In the 1940s, Richard Feynman and Ernest Stueckelberg independently developed a notation (now known as Feynman Diagrams), that greatly ease certain calculations in QFT.

Julian Schwinger complained that Feynman had made QFT accessible to the “masses”. He meant the “masses of physicists.” Between this post and the next, we’re going to take Feynman one better and make Feynman diagrams accessible to the masses, as in “masses of amateurs.” Our simplification will be to use qubits. For a reference in the arXiv literature, see Quantum Electrodynamics for Qubits, but our discussion will be simpler than this. This post will discuss Feynman diagrams the usual way.

I will try to write this introduction at a low enough level, and with enough links to explanations of the jargon, that it can be understood by people unfamiliar with particle physics. Accordingly, we will skim over a lot of details, but will include links to articles that will explain further, if needed.

The Bilson-Thompson Helon (Braid) Model

In 2005, Sundance O. Bilson-Thompson wrote hep-ph/0503213v2, an arXiv paper titled “A topological model of composite preons”. The paper gave a preon model of quarks, leptons, and gauge bosons. That is, it modeled these particles as composite particles made up of preons. The preons he used were elements of the braid group B_3. A later paper by Sundance O. Bilson-Thompson, Fotini Markopoulou, and Lee Smolin showed that these states can be obtained from background independent models of quantum spacetime that “propagate coherently as they can be shown to be noiseless subsystems of the microscopic quantum dynamics”.

Since I play with a similar preon model, I thought I would comment on this theory from my perspective. I’ve given links to a few of the technical terms, but this post is not going to make a lot of sense to those not already playing with particle physics.

Measuring the Speed of Gravity (Waves)

Newton’s equations give the speed of gravity as infinite. For example, in Cartesian coordinates, suppose a gravitating mass 2M is at the origin up until time t=0.  At that time, the mass splits into two masses of mass M, one going in the +x direction at speed v the other in the -x direction at speed v. For times greater than 0, the gravitational potential is given by the sum of the two gravitational potentials:

(1)

At any distance, the above depends on t so the gravitational potential (and it is easy to show the gravitational force) is instantaneously changed at all distances from the origin. The speed of gravity is therefore infinite in Newton’s theory.