Bound States as Symmetry Operators and E8

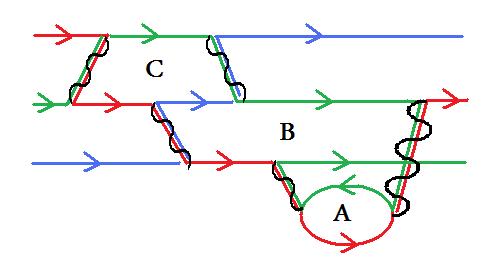
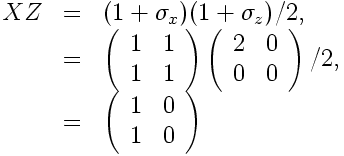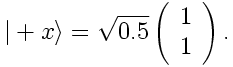Previously, we saw that density operators generate symmetries in the set of quantum states and that these new symmetries gave non Hermitian quantum states. We then saw that bound states of Feynman diagrams can be represented by matrices of these non Hermitian quantum states. In this post, we use these matrices of non Hermitian quantum states, that is the bound states, to generate symmetries on all the quantum states, bound and free. This is necessary for the recursion that derives E8 as a consequence of treating bound states on an equal footing with free states.

The method of turning a matrix of density matrix states into a symmetry on matrices of density matrix states follows exactly our method of turning a density matrix into a symmetry of density matrices. Let U and V be arbitrary 3×3 matrices whose entries are complex multiples of density matrix states, and let S be an arbitrary 3×3 density matrix whose entries are complex multiples of density matrix states. Since S is a density matrix we have SS = S. The transformation on U is:

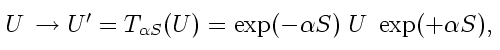
and the transformation on V is similar. As in the earlier density matrix case, this transformation preserves addition and multiplication, that is:

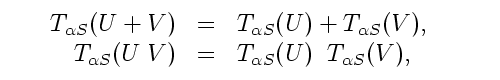
since the transformation is linear, that is, , and in the case of multiplication, the exponentials between the products cancel.

Bound States as Density Matrices

Review: Previously, we showed that non Hermitian density matrices arise naturally as the result of using density matrices to define symmetry operations on density matrices, and that these sorts of things might be used in defining Feynman diagrams modeling bound states. We begin with a proton modeled as a set of three valence quarks held together by gluons:

We cut the gluon lines and look only at the valence quarks (as it is these that determine the quantum numbers of the bound state). This gives us a simplified model:

To model this from density matrices requires a simple sort of Feynman propagator, one that corresponds to a non Hermitian density matrix:

The corresponding non Hermitian density matrix is a product of two pure Hermitian density matrices. Let us assign to the colors red, green, and blue, the density matrices for spin in the +x, +y, and +z directions, respectively. Then, for example, the above propagator becomes:

In the remainder of this post we take Feynman diagrams like this, and assemble them into density matrices that represent the bound state. (They will be 3×3 matrices of Feynman diagrams or, equivalently, 3×3 matrices of non Hermitian density matrices.)

Non Hermitian Density Matrices

Recently Garrett Lisi’s used a broken E8 symmetry to classify the known elementary particles. I believe that E8 arises naturally from composite particles. The outline of the argument (as covered in the first post) amounts to noticing that E8 is unique among the simple Lie algebras in that “in the context of linear algebra, E8 is most simply described as the group of symmetries of its own Lie algebra!”

In the second post in this E8 series, I showed how particle states could be used as symmetry generators for certain symmetries of the particle states. This was done using pure density matrices. We began with a certain symmetry of the Clifford algebra of the Pauli algebra, and turned that symmetry into one of the pure density matrices of the Pauli algebra. In effect, we got the quantum states to operate on themselves to make other quantum states, exactly the sort of thing that is necessary to build E8.

We want to add composite or “bound” states to the “free” states that are represented by the usual pure density matrices. We will then add these bound states to the usual pure density matrices to create a larger algebra. (In that algebra, multiplication of states with differing numbers of particles will give zero.) The bound states will also be represented as density matrices. In this post we will lay the foundations for describing bound states by very simple Feynman diagrams, it will be collections of these Feynman diagrams, formed into matrices, that will create the density matrices for the bound states.

Quantum States as Symmetry Operators

The first step in seeing how a broken E8 can arise by treating composite particles as if they were elementary consists in understanding how it is that a quantum state can be interpreted as a symmetry operator. That is the subject of this post. The remaining steps are outlined in the previous post.

We begin with the Pauli algebra. Since this is an introductory post, we will use the notation the majority of my readers have already learned, that of the Pauli spin matrices and Pauil spinors. I have found that students learn best by example, so we will turn the spinor for spin in the +x direction into a symmetry operator on the quantum states of the Pauli algebra:

Broken E8 as a Result of Composite Particles I

Since I think that the standard model particles are composite, it’s natural, with Garrett Lisi’s use of E8, to wonder if E8 can arise naturally as a result of composite particles. I think it can. I will use the fact that as Baez puts it, “This means that in the context of linear algebra, E8 is most simply described as the group of symmetries of its own Lie algebra!”

This suggests that we begin with the Pauli algebra and write down its (well known) quantum states, that is, the 2×1 spinors or the pure density matrices. In order to allow ourselves to bootstrap the states, instead of thinking of the base algebra as the Pauli algebra, we think of the base algebra as these quantum states, that is, we use Schwinger’s measurement algebra. In the measurement algebra, the primitive elements correspond to elementary particle quantum states. To get the power of the Clifford algebra, you can still define the Clifford algebra canonical basis vectors in terms of the measurement algebra.