Quantum States as Symmetry Operators

The first step in seeing how a broken E8 can arise by treating composite particles as if they were elementary consists in understanding how it is that a quantum state can be interpreted as a symmetry operator. That is the subject of this post. The remaining steps are outlined in the previous post.

We begin with the Pauli algebra. Since this is an introductory post, we will use the notation the majority of my readers have already learned, that of the Pauli spin matrices and Pauil spinors. I have found that students learn best by example, so we will turn the spinor for spin in the +x direction into a symmetry operator on the quantum states of the Pauli algebra:

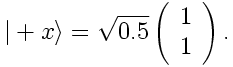
First convert the spinor into a density matrix. We do that by multiplying the ket spinor by the bra spinor:

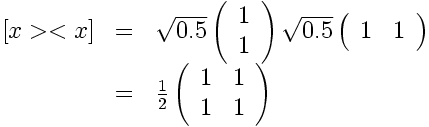
The Pauli algebra is generated by the three matrices . Suppose that we transform these three matrices to three new matrices, . The transformation is a symmetry of the algebra if all possible equations we could write with the old Pauli matrices are equally satisfied with the new Pauil matrices.

It is easy to show that if we begin with any 2×2 matrix M and have a real number, then the transformation of the Pauli algebra given by the following is a symmetry:

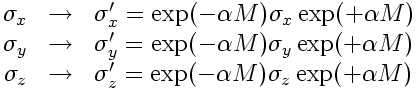
In short, the above transformation is a symmetry of the Pauli algebra because it (a) maps matrix 0 to matrix 0, (b) maps matrix 1 to matrix 1, (c) is linear so it preserves matrix addition, and (d) the exponentials cancel so it preserves multiplication. This happens regardless of the value of .

We can label the above transformation . And it is easy to see that this transformation is a 1-parameter subgroup of the symmetry group of the Pauli algebra with as the paramter. That is, . A natural continuation of the story is to then note that when you differentiate the transformation with respect to , you induce a commutator bracket on the algebra. That is:

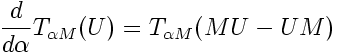
but our interests lie with the quantum states rather than the Lie algebra.

So let’s see what happens when we compute , the transformation induced by the first Pauli spin matrix. In order to make the calculation, let’s first calculate the exponential. Recalling that , we find that:

As , the above exponential also goes to infinity as . To keep it finite, we can multiply it by :

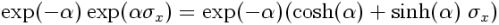
In fact, commutes with , so we can combine the two exponentials into a single exponential, that is, . That keeps the product finite in the limit of + infinity. (To keep it finite in the limit of – infinity, we would instead have to multiply by .)

And what is the limit of as ? Since and , we have that goes to . But this just our density matrix for spin in the +x direction:

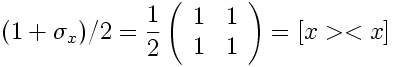
The Symmetry Transformation

I guess we should work out exactly what symmetry operation is. To do this, it helps to know the following easily proven commutation rules:

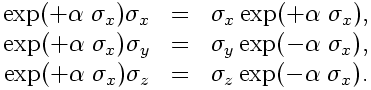
and similarly for the various permutations of . The above rules allow us to compute the effects of on the basis vectors of the Pauli algebra as follows:

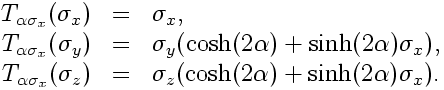
Upon taking the limit as , the cosh and sinh terms exponentially approach, well, an exponential. Factoring that exponential out, we have that the factor on the right of the y and z transformations approaches . That is, they become an exponential times the +x spin density matrix. Of course this sort of thing is not special with x, it is also true for any other vector in the Pauli algebra.

Summing up so far, a quantum state of the Pauli algebra can be put into a (pure) density matrix form. That density matrix defines a symmetry transformation of the Clifford algebra. But in order for our E8 bootstrap to work, we need to move that transformation over to the quantum states themselves. That is, we want the symmetry transformation produced by the density matrix to be a symmetry transformation of the density matrices.

To do this, we need only note that the density matrices are made from the Clifford algebra. Since we’ve shown that the density matrix creates a symmetry operation on the Clifford algebra, this also implies a symmetry operation on the density matrices. More generally, if we assume that the density matrices (i.e. the quantum states) are fundamental, we can derive the Clifford algebra from those states by subtraction. For example, the difference between the density matrices for spin in the +x and -x directions is :

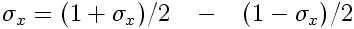
Thus we can treat the “density matrix algebra” as the fundamental algebra instead of the Pauli algebra. This density matrix algebra includes all products and sums of density matrices, and since these include the three Pauli spin matrices, this also includes the entire Pauli algebra.

The above derivation shows a very small amount of why this is the case. A more complete discussion is available in my incomplete web book on density operators. In that book, we eventually drop the messy matrix notation and work with pure algebra.

Using the density matrices as an algebra is an example of Julian Schwinger’s Measurement Algebra. For more information on this, it is probably best to read the original paper by Schwinger on this subject. For a long time, I maintained a wikipedi at at the Measurement Algebra website that gave links to web copies of the original paper. It didn’t seem to me that anybody was getting any good out of it, so when it got infested by World of Warcraft fans and I deleted it. When I get back to Seattle I will put the links in here and on the MA webpage. And by reading this far, you now understand why it is that I put the E8 applet on the measurement algebra website.

The general form for a pure density matrix of the Pauli algebra is which gives spin in the direction. Looking at this as a basis for general transformations of the pure density matrices, we have only found 3 degrees of freedom, that is, the transformations associated with plus linear combinations of these. We have not even exhausted the symmetry transformations that can be put into the form where M is a 2×2 matrix.

On our next post we will discuss the symmetry transformations of the sort . We will interpret these transformations as being generated by “gauge bosons” that act on the pure density matrices to convert them from one spin orientation to another. This will give us a total of 6 degrees of freedom in our symmetries of the pure density matrices. We will add these gauge bosons to our pure density matrix particles giving us a 6 dimensional manifold of particle states, and a 6-dimensional Lie algebra of symmetries of those particle states, namely the symmetries generated by the Pauli spin matrices and products of two Pauli spin matrices.

But our 6 particle states have more symmetry than is exhausted by their own pitiful 6-dimensional efforts, and we will associate these more complicated symmetries with yet more particle states, states that we will interpret as bound states of the original pure density state and the “gluons.” And so we climb slowly towards E8, which has quite a bit more dimensions. But there we will run out of unused symmetries of the particles, and so run out of the ability to create new particle states by turning symmetries into particles.