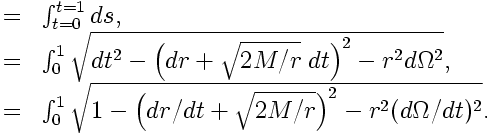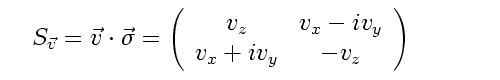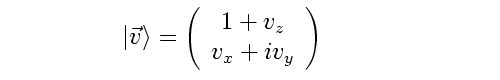The first problem in writing gravitation as a particle interaction is the fact that QFT works best on flat space, while general relativity is almost always written in arbitrary coordinates. One of the underlying principles of general relativity is that coordinates shouldn’t matter (background independence), so this problem appears to be a deep one. The point of view we will take here is that of the “new physics” .
That is, we will treat the equations of the old physics with more respect than we treat their theories. Consequently, instead of chasing after will-o-the-wisps like background independence, we will instead search for a method of writing general relativity using the mathematical tools of quantum field theory. Very fortunately for us, that method has already been found; it is the gauge theory of gravity discovered by the Cambridge Geometry Algebra Research Group. The purpose of this post is to introduce the theory to those who have not yet been exposed to it, and to note that this gravity theory (which is identical to GR so long as you restrict your attention to stuff that happens outside of the event horizons of black holes) picks out Painleve coordinates as a natural flat space (and therefore QFT compatible) coordinate system for a non rotating black hole.
Those with a graduate education in physics are already familiar with the Geometric Algebra (GA) in that it is equivalent to the Gamma matrices used throughout quantum field theory. So a gravitation theory that is equivalent to general relativity, but is written with gamma matrices, is a natural starting point for a search for a unified field theory.
The primary proponent for the use of GA in physics (outside of QFT) is David Hestenes, who applied it to classical and quantum mechanics. As the introduction to GA article at the Cambridge Geometry group’s website puts it:
We believe that there are two aspects of Hestenes’ work which physicists should take particularly seriously. The first is that the geometric algebra of spacetime is the best available mathematical tool for theoretical physics, classical or quantum. Related to this part of the programme is the claim that complex numbers arising in physical applications usually have a natural geometric interpretation that is hidden in conventional formulations. David’s second major idea is that the Dirac theory of the electron contains important geometric information, which is disguised in the conventional matrix based approaches.
Now that’s a pretty big claim: that geometric algebra is the best mathematical tool for all physics. I will spend the rest of this post exploring this claim in the case of general relativity, and then tracing the consequences for a unified field theory.
Continue reading →
Filed under gravity, physics

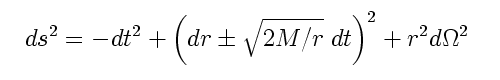 . Let’s let our path start at time t=0 and end at time t=1. For the path to be a geodesic, we must extremize the following integral (I’ll quickly sneak in a minus sign to make the path be timelike instead of spacelike):
. Let’s let our path start at time t=0 and end at time t=1. For the path to be a geodesic, we must extremize the following integral (I’ll quickly sneak in a minus sign to make the path be timelike instead of spacelike):