Precolor and Black Holes and all that.

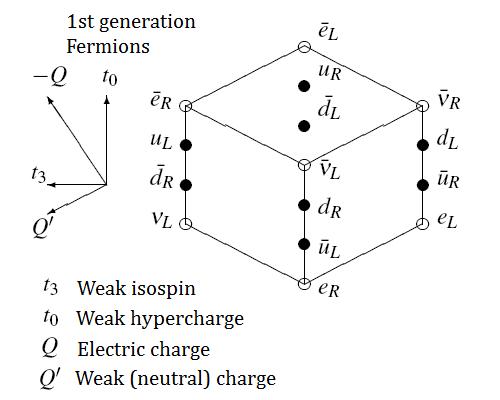
In the comments to my previous post, Tony Smith asked where color came from in my use of the Clifford algebra C(4,1) as I didn’t explain it in my previous post. This is one of the 30 or so topics on which my guesses for the physics of sub elementary particles differs drastically from mainstream physics.

Crack(pot)s in the Foundations

The problem with making drastic changes to the foundations of physics is that the foundations are tightly woven together with very long threads. When you pull a thread out, you find that there is a neat whole left which just happens to be exactly the size and shape of the thread you pulled out. When you try to weave a new thread in a new direction starting in part of the hole left by the one you yanked out, you find that there are many other threads that get in the way. You have to pull those threads out too. And then these changes cascade to yet more changes.

By the time you are done, you will find that you have to rewrite the foundations completely. This is why people who mess with the foundations of physics are thought of as crackpots; they almost always are.

Precolor and Primitive Idempotents

An idempotent is an element of an algebra that is unchanged when it is squared, . In an algebra, the “primitive” idempotents are those that cannot be written as sums of nonzero idempotents. In a sense, these are like primes. In the density matrix formulation of quantum mechanics, the particle states are primitive idempotents.

1-parameter subgroups of Lie groups

My first cut at this post was a fairly traditional introduction to one parameter subgroups of Lie groups. Along the way, I made this illustration showing the complicated global versus simple local behavior of one parameter subgroups:

But then, in writing down examples, I realized that the readers are likely to be intimately familiar with the multiplication of complex numbers, and so I decided to concentrate on the multiplication of nonzero complex numbers. These form a nice (real) 2-dimensional Lie group with very clear one-parameter subgroups.

So I decided to rewrite the post using simple examples only. You can get the abstract Lie theory from wikipedia, but I had to include the above illustration cause it’s too pretty to put in the bit bucket.