Quarks, leptons and generations!

I’ve finally just now figured out how to combine the quark / lepton weak hypercharge and weak isospin quantum numbers with the generation numbers. This should allow the Koide mass formula to be extended to the quarks!

The weak hypercharge and weak isospin quantum numbers for the elementary fermions are:
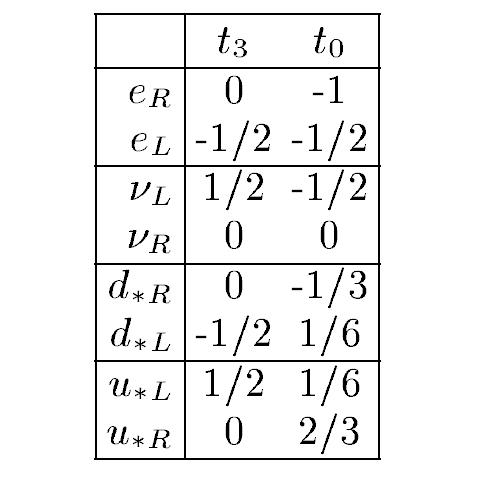, with the quantum numbers for the antiparticles with opposite handedness given by the negatives of the above.

The Koide mass formulas for the charged and neutral leptons can be derived from making the assumption that these particles are color neutral composite particles built from three preons that I’ve usually called “snuarks” and they are taken from a set of three mutually unbiased bases for the Pauli algebra.

In the density matrix language, a particle is not represented by a state vector, but instead by a state matrix. A state matrix gives the transition amplitudes for the states that are bound together. The diagonal entries correspond to the amplitude for the propagation of one of the snuarks without change. The off diagonal entries give amplitudes for the various ways a snuark can switch states. Consequently, in the language of quarks and gluons, the off diagonal entries represent the gauge bosons of the theory while the diagonal entries give the valence quarks. Using “r,g,b” as the indices for the matrix, the (r,g) entry gives the amplitude for transitions from G to R; in the quark / gluon language, this would be the action of a R/G gluon.

For the Koide formula, one assumes that the gluons are symmetric with respect to color. This makes the 3×3 matrix into a circulant matrix. Next, the bound state is required to be consistent as a quantum particle. In the density matrix language, that means placing the same requirements on the 3×3 matrix as one normally applies to a pure quantum density matrix state; idempotency (i.e. BB = B). To solve this problem, one rewrites the idempotency equation for circulant matrices:

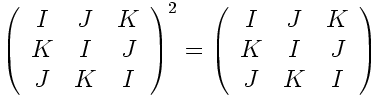
into 3 coupled quadratic equations in the 3 complex unknowns I, J, and K:

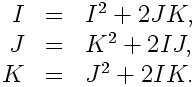
After a little college algebra, one finds that there are 8 solutions in the complexes to the above equations:

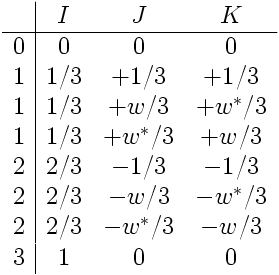
where . The 8 solutions are labelled “0”, “1”, “2”, or “3”. These numbers are the traces of the matrix, and correspond to the number of particles present in the solution. In other words, the first line, where I=J=K=0, corresponds to no particles present. The next three lines give the single particle solutions (which is what we are interested in). The next three lines are sums of two different single particle solutions, and the final line is the sum of all three single particle solutions.

Physically, the entries in the 3×3 matrix are not complex numbers but are Feynman diagrams; ask Kea for the reference in the literature to this slight and obvious generalization of Feynman diagrams. To get the Koide formula, one sums over the scalar parts of these 3×3 = 9 diagrams. The square root of 2 and the exp(i pi/12) comes from Berry phase, while the exp(2i/9) comes from QFT corrections for infrared divergence. The obvious quantum numbers for the generations are the cubed roots of unity. That is, one has and 1 as the quantum numbers for the three generations.

Quark and Lepton Idempotency Equation

The notion of “idempotency” that worked for the Koide equation has a natural generalization for the quarks. Instead of making the assumption that the 3×3 matrices are circulant, we let the 3×3 matrices be more arbitrary. But we still require that the new matrices satisfy BB = B. And we expect to see a generation structure. So we expect to get solutions in groups of 8 where different numbers of particles (from 3 different generations) are included.

The new idempotency equations have to give the right weak hypercharge and weak isospin quantum numbers. The Koide equation was for the mass interaction between left and right handed leptons. The reason idempotency works for this is that one can make the transition between left and right any number of times, the result needs to be the same. For the quark and lepton structure, we want to look for the propagating structure, that is, we want to look for the handed quarks and leptons individually. This also satisfies an idempotency equation; a propagating left handed quark remains a left handed quark. So the same idempotency equation should work for the chiral particles as works for their masses.

From a density matrix point of view, a bound state is a collection of things (sums of Feynman diagrams) that can happen to the snuarks with various amplitudes for the various possibilities. Keeping track of the colors of the three preons, which I will label “R,G,B,” these 3 colors can be permuted in 6 ways which I will label as follows:

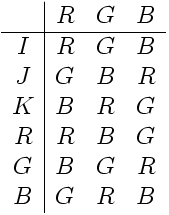
As permutations, these satisfy the usual equations for the permutation group on 3 elements and they can be represented by 3×3 matrices with entries taken from 0 and 1 in the usual way.

Now we add a new feature: Since the permutations are Feynman diagrams, they can also include an arbitrary complex phase. So this raises the question: “suppose that the permutations are made complex, what values can be assigned to them so that they still satisfy the usual permutation group relations?” We will keep the phase of I unchanged. Since J cubes to unity, that is, JJJ = I, the only possibility for an arbitrary phase for J is a cubed root of unity. It turns out that there are three solutions for the “complex permutation group on 3 elements” as follows:

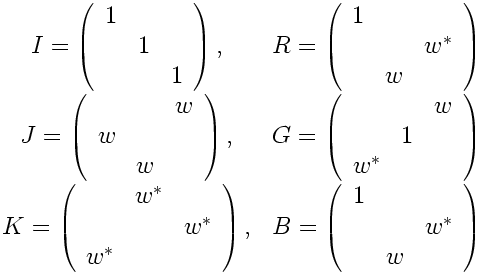
When one chooses w=1, the above 6 matrices give the group of permutations on 3 elements with no phases. With w a complex cubed root of unity, one obtains two more copies of the permutation group. And now the off diagonal entries give the generation structure for Koide’s formula. Consequently, if we assign R=G=B=0, we will get the circulant matrices that work for the leptons. The generation structure shows up in the choice of repersentation of the permutation group.

Weak Hypercharge Quantum Numbers

As before, to get the quantum numbers of the bound states we apply the idempotency equation to give a coupled set of quadratic equations. Only now, instead of quadratic equations in I, J, and K, our equations are in I, J, K, R, G, and B:

The above six coupled quadratic equations are fairly difficult to solve. The natural quantum number to associate with weak hypercharge is I, as weak hypercharge is a U(1) symmetry. Sure enough, I gives just the right values for weak hypercharge, {1, 2/3, 1/2, 1/3, 1/6, 0}. The antiparticles will then give the minus values. The detailed solution to the coupled quadratic equations, along with the assignments to the elementary particles is in an incomplete paper of mine from 2007, dmfound.pdf around pages 35 to 39.

Perhaps this will allow the Koide mass formula to be generalized to the quarks; work in progress.

It is also possible that this will allow the generation quantum numbers to be unified with the weak hypercharge and weak isospin quantum numbers in a manner that will be compatible with Lisi’s E8 assignments. For the weak hypercharge and weak isospin quantum numbers in Lisi’s paper, see table 4 page 12 of 0711.0770 see table 4 page 12. In his notation, the quark and lepton weak hypercharge (1/2Y) and weak isospin (W^3) quantum numbers for one column of the Fermion cube are as follows:

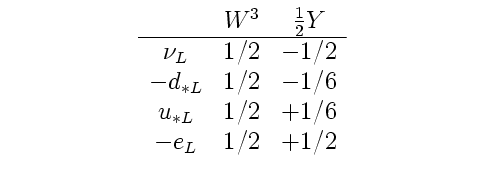
where “-” indicates the anti particles.